Paper in IEEE Transactions on Signal Processing
© 2018 EPFL
06.08.2018 “Efficient Multidimensional Diracs Estimation With Linear Sample Complexity” by Hanjie Pan, Thierry Blu and Martin Vetterli
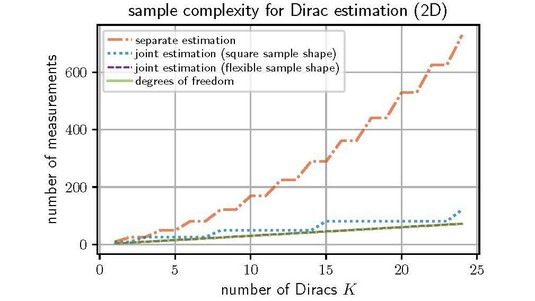
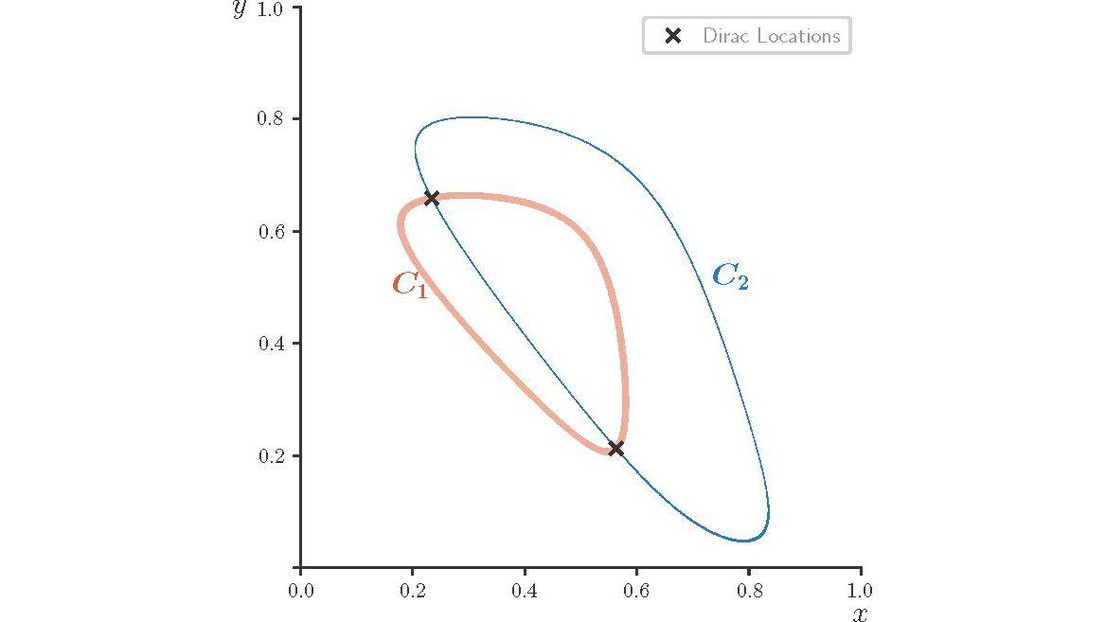
Abstract: Estimating Diracs in continuous two or higher dimensions is a fundamental problem in imaging. Previous approaches extended one-dimensional (1-D) methods, like the ones based on finite rate of innovation (FRI) sampling, in a separable manner, e.g., along the horizontal and vertical dimensions separately in 2-D. The separate estimation leads to a sample complexity of O(K^D) for K Diracs in D dimensions, despite that the total degrees of freedom only increase linearly with respect to D. We propose a new method that enforces the continuous-domain sparsity constraints simultaneously along all dimensions, leading to a reconstruction algorithm with linear sample complexity O(K), or a gain of O(K^{D−1}) over previous FRI-based methods. The multi-dimensional Dirac locations are subsequently determined by the intersections of hypersurfaces (e.g., curves in 2-D), which can be computed algebraically from the common roots of polynomials. We first demonstrate the performance of the new multidimensional algorithm on simulated data: multidimensional Dirac location retrieval under noisy measurements. Then, we show results on real data: radio astronomy point source reconstruction (from LOFAR telescope measurements) and the direction of arrival estimation of acoustic signals (using Pyramic microphone arrays).

Published in: IEEE Transactions on Signal Processing Volume: 66, Issue: 17.