Étudier les oscillations des solitons
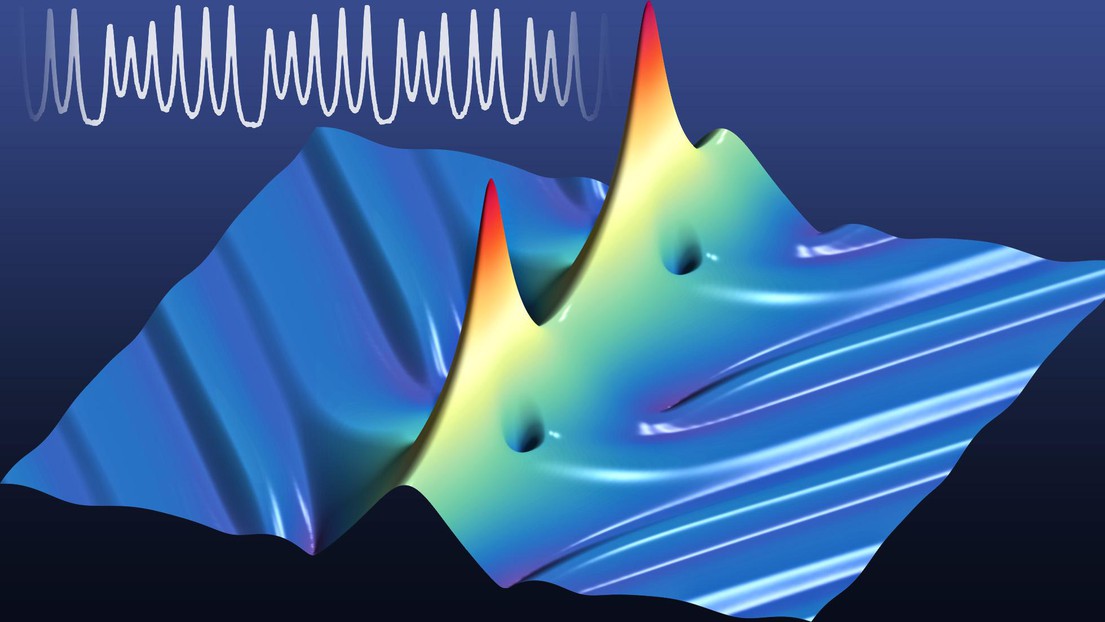
Simulation numérique de l’évolution d’un soliton oscillant et mesures des oscillations. © Erwan Lucas
Des scientifiques de l’EPFL ont étudié les instabilités complexes des solitons optique dans des micro-résonateurs, montrant des similitudes avec une multitude de systèmes dynamiques.
En optique, un soliton dissipatif consiste en une impulsion lumineuse qui circule sans se déformer. Cela résulte d'un équilibre entre deux effets qui se compensent : d'une part, la dispersion du milieu de propagation tend à élargir la durée de l'impulsion, mais est compensée par la nonlinéarité de Kerr, qui la re-compresse, alors que d'autre part, les pertes lors de la propagation, qui tendent à affaiblir l'impulsion, sont contrebalancées par le gain fournit par un laser. Les chercheurs de l'EPFL emprisonnent ces solitons dans une cavité optique, de façon à ce qu'ils « tournent en rond », ce qui simplifie leur étude. Par ailleurs, ces solitons en cavité ont récemment attiré un grand intérêt car ils permettent de générer des trains d'impulsions lumineuses ultra-rapides, trouvant des applications en spectroscopie ou en métrologie fréquentielle (peignes de fréquence optique).
Dans certaines conditions d'opération, cette double compensation est dégradée et l'impulsion se trouve déstabilisée et commence à osciller, avant de s'effondrer et disparaître, résultat d’une bascule de l’équilibre du système. Ce genre d’instabilité est caractéristique des systèmes dynamiques non-linéaires et a déjà été observé dans des lasers proche de leur seuil d’émission ou bien même dans l’évolution du nombre d’individus d’une espèce (modèle proie-prédateur de Lotka-Volterra) et dans les changements climatiques. Dans tous ces cas, des signes avant-coureurs, tels que le ralentissement des oscillations, permettent de prévoir, dans une certaine mesure, une transition critique du système (comme l’extinction d’une espèce).
L’intérêt du système optique, c’est que les échelles de temps sont très rapides et qu’un grand nombre réalisations peuvent donc être étudiés. Récemment, l’équipe du Professeur Kippenberg a perfectionné les méthodes de contrôle du système optique permettant de conduire les expériences avec des paramètres bien définis. Dans ces nouveaux travaux, Erwan Lucas et ses collègues induisent de façon déterministe les oscillations du soliton et observent directement la dynamique spatio-temporelle. Leur étude valide expérimentalement les prédictions des modèles numériques, notamment sur le ralentissement critique du système et son évolution vers le chaos.
« Il est vraiment fascinant de voir qu’un un système apparemment simple peut manifester une dynamique si complexe ! » s’enthousiasment les membres de l’équipe. A mesure que le soliton devient de plus en plus instable, l'amplitude des oscillations augmente et leur fréquence diminue, tandis que le motif d'oscillation devient de plus en plus incohérent et complexe. L’étude a également permis de mettre en évidence que plusieurs solitons peuvent interagir et synchroniser leurs oscillations.
Ces observations apportent une validation expérimentale des modèles d’optique non-linéaires. Les méthodes développées par les scientifiques constituent également une palette de diagnostiques pour prévenir ces instabilités des solitons et garantir une opération stable des peignes de fréquences.
Référence
E. Lucas, M. Karpov, H. Guo, M. L. Gorodetsky, T. J. Kippenberg. Breathing dissipative solitons in optical microresonators.Nature Communications 8, 736 (2017). DOI: 10.1038/s41467-017-00719-w