Distributionally robust state estimation can be computed in real time
© 2023 EPFL
The manuscript entitled "Regularization for distributionally robust state estimation and
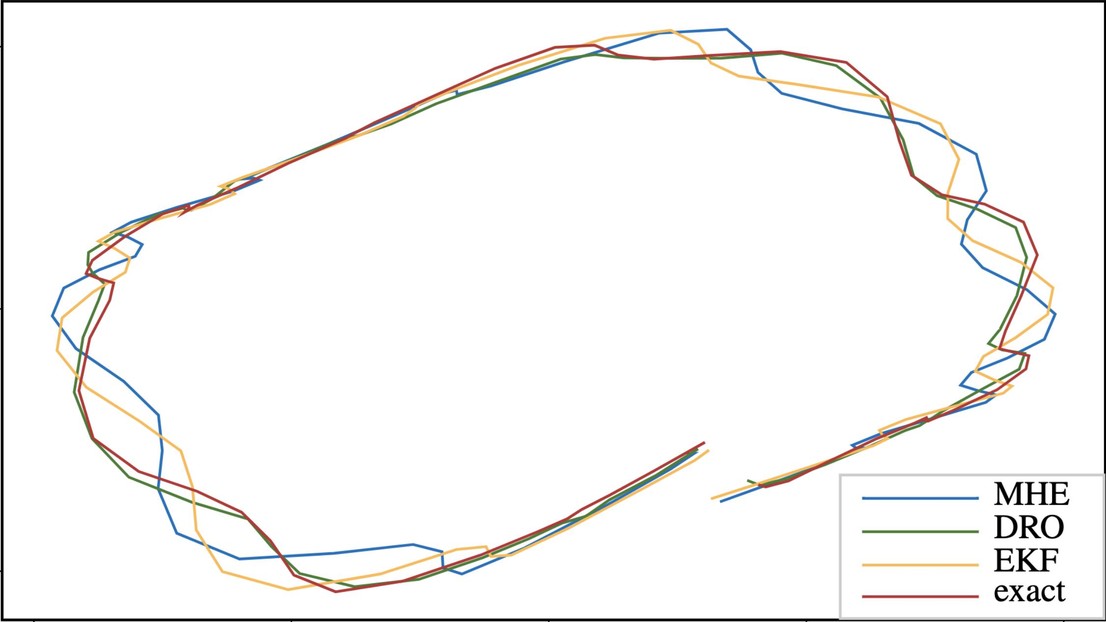
prediction" has been accepted for publication in the Control Systems Letters journal. It describes how one can use regularization to minimize the mean absolute error of state estimates when the system is affected by noise distributed according to a distribution of which only samples are known. By design, the method is designed offline and provides out-of-sample guarantees when deployed in the field.
The increasing availability of sensing techniques provides a great opportunity for engineers to design state estimation methods, which are optimal for the system under observation and the observed noise patterns. However, these patterns often do not fulfill the assumptions of existing approaches. We provide a direct method using samples of the noise to create a moving horizon observer for linear time-varying and nonlinear systems, which is optimal under the empirical noise distribution. Moreover, we show how to enhance the observer with distributional robustness properties in order to handle unmodeled components in the noise profile, as well as different noise realizations. We prove that, even though the design of distributionally robust estimators is a complex minmax problem over an infinite-dimensional space, it can be transformed into a regularized linear program using a system level synthesis approach. Numerical experiments with the Van der Pol oscillator show the benefits of not only using empirical samples of the noise to design the state estimator, but also of adding distributional robustness. We show that our method can significantly outperform state-of-the-art approaches under challenging noise distributions, including multimodal and deterministic components.