Breathing optical solitons
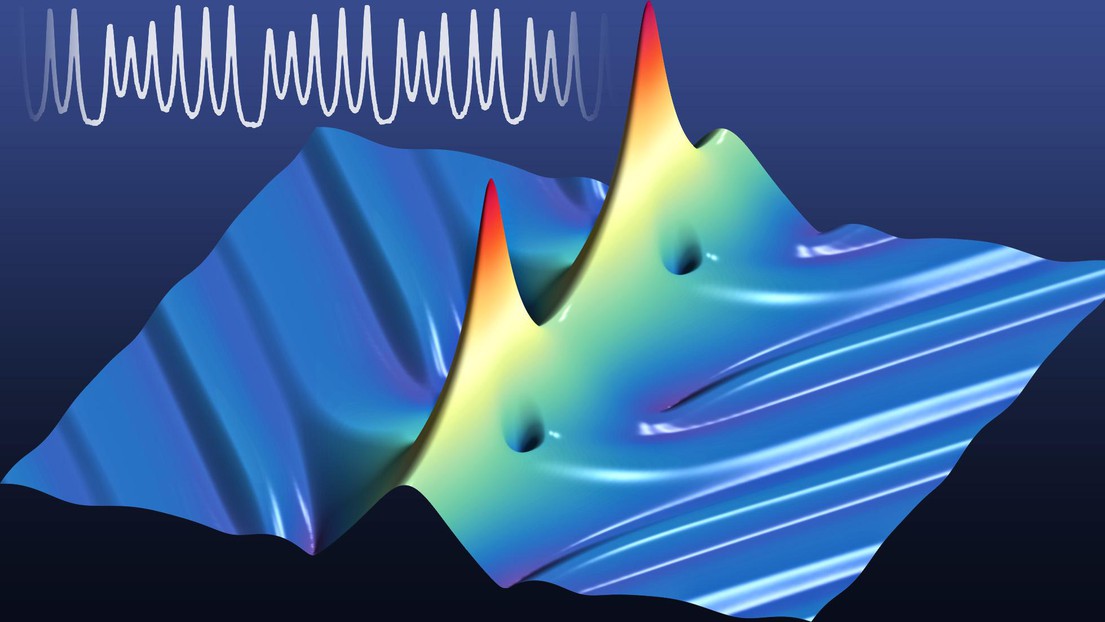
Numerical simulation of the evolution of a breathing soliton and measured oscillations. © Erwan Lucas
Scientists at EPFL have studied the complex instabilities of optical solitons in micro-resonators, showing similarities with a variety of dynamical systems.
In optics, a dissipative soliton consists of a light pulse that travels without deformation. This results from a balance between two counterbalancing effects: on one hand, the dispersion of the propagation medium tends to lengthen the pulse duration, but this is offset by the Kerr-nonlinearity, which compresses it again, while on the other hand, the propagation losses, which tend to weaken the pulse, are counterbalanced by the gain provided by a laser. EPFL researchers trap these solitons in an optical cavity, so that they "go round in circles", which simplifies their study. In addition, these cavity solitons have recently attracted great interest because they can generate ultra-fast trains of light pulses, finding applications in spectroscopy or frequency metrology as they constitute optical frequency combs.
Under certain operating conditions, this double compensation is degraded and the soliton is destabilized and begins to oscillate – scientists call it breathing – before collapsing and vanishing, owing to a tipping point in the equilibriums of the system. This type of instability is characteristic of non-linear dynamical systems and has been also observed in the dynamics of lasers near threshold, and even the evolution of species populations (Lotka-Volterra prey-predator model) or in the climate. In all these cases, early warning signs, such as the slowing of the oscillations, helps to some extent to predict a critical transition of the system (such as the extinction of a species).
The advantage of the optical system is that the time scales are very fast and a large number of realizations can be studied. Recently, Professor Kippenberg's team has improved the control methods of the optical system allowing experiments to be carried out under well-defined parameters. In this new work, Erwan Lucas and his colleagues deterministically induce soliton breathing and directly observe the spatio-temporal dynamics. Their study experimentally validates the predictions of numerical models, notably on the critical slowing down of the system and its evolution towards chaos.
“It is truly fascinating to see that a seemingly simple system can exhibit such complex dynamics! " explain the team members. As the soliton is more and more unstable, the amplitude of the oscillations increases and their frequency reduces, while the oscillation pattern becomes more and more incoherent and complex. The study also demonstrated that several solitons can interact and synchronize their oscillations.
These observations provide experimental validation of non-linear optical models in the unstable case. The methods developed by the scientists also provide a range of diagnoses to prevent these solitons instabilities and ensure a stable operation of the frequency combs.
Reference
E. Lucas, M. Karpov, H. Guo, M. L. Gorodetsky & T. J. Kippenberg. Breathing dissipative solitons in optical microresonators.Nature Communications 8, 736 (2017). DOI: 10.1038/s41467-017-00719-w